이번 문제는 내 힘으로 못 풀었고, 위와 비슷한 개념의 문제를 해결한 아래 블로그에서 어떻게 푸는지 공부하였고, 이에대해 내가 이해한 바 이다. https://jaimemin.tistory.com/547
static int table[10][100 + 1][1 << 10];
static int N;
static int __solution(int start, int length, int big_bit)
{
if (start < 0 || start > 9) //범위를 넘는 수.
return 0;
if (length == N) //원하는 길이에 도달 함.
return ((big_bit == (1 << 10) - 1) ? 1 : 0); //모든 숫자가 존재하면 1로 반환하여 카운트 시키고,
//그렇지 않으면 0을 반환하여 카운트에서 제외함.
int &ret = table[start][length][big_bit];
if (ret >= 0) //cache hit,
return ret;
//cache miss,
int ret1 = __solution(start - 1, length + 1, big_bit | (1 << (start - 1))) % 1000000000;
int ret2 = __solution(start + 1, length + 1, big_bit | (1 << (start + 1))) % 1000000000;
return (ret = (ret1 + ret2) % 1000000000);
}
static int solution(void)
{
int ret = 0;
scanf("%d", &N);
memset(table, -1, sizeof(table));
for (int start = 1; start <= 9; start++)
{
ret += __solution(start, 1, 1 << start);
ret %= 1000000000;
}
return ret;
}먼저 이 문제를 해결하기 위해서는 https://www.acmicpc.net/problem/10844 이 문제에 대한 이해가 선행되어야 하는 것 같다. 해당 문제에 풀이에 대하여 간단히 정리하면 아래와 같다.
1로 시작하는 길이가 4인 계단수를 구하고자 한다면 아래와 같은 흐름이 된다.
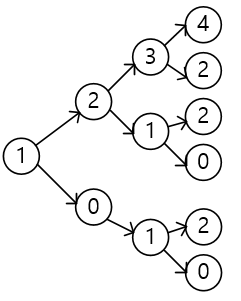
그래서 이러한 작업을 재귀적으로 구현하고, 이를 1 부터 9까지 반복해서 실행하면 되는 것이다.
또한 3번째 단계에서 4번째 단계로 넘어 갈 때 동일한 작업이 발생하는 것을 볼 수 있다. 이러한 작업은 이미 한 것이기 때문에 다시 할 필요가 없고 이에대한 정보를 기록하여 사용하면 되기 때문에 성능을 개선 할 수 있다.
그래서 이번 문제는 이러한 개념이 확장된 것으로 보면 되고 그것이 0 부터 9 까지 모든 숫자가 계단수에 들어가야 된다는 조건이다.
이는 bit mask / bit map 개념을 이용하여 해결 할 수 있다.
00010100 이라는 이진수가 있을 때, 특정 비트 값이 설정되었는지 확인 하고자 한다면 00010000과 AND 시키면 쉽게 구할 수 있다. 굳이 0번째 bit부터 마지막 bit까지 일일이 확인 할 필요가 없다는 것이다.
이제 table이 어떤 식으로 활용되는지 살펴보면,
table[시작하는 값][현재 길이][0 ~ 9 까지 존재하는지] 이다.
즉, 주어진 조건을 만족하는 숫자 중 3으로 시작하며 그 길이가 12 인 것들 의 개수를 알고 싶으면
table[3][12][?] 로 접근하면 되는 것이다. 여기서 ?에 들어가는 것이 앞서 언급한 bit mask의 개념이 적용된다.
int 하나를 하나의 bit로 보는 것이다.
그래서 1 << 10 은 1024 이지만 0 ~ 9 까지 모든 값이 설정되어 있는지 여부를 보기위한 10bit 짜리인 자료로 생각하면 된다.
그래서 __solution() 이 맨 처음 호출 될 때, 1 << start 로 하여 start 하는 숫자의 bit 값을 설정하고,
이후 재귀적으로 호출 될 때 bit_bit (현재 bit) 에 다음에 확인 할 수 에 대한 bit를 설정하기 위해 OR 연산을 해주는 것이다.
이런식으로 재귀적으로 호출 되다가 우리가 원하는 길이에 도달 하였을 때, 모든 숫자가 존재하는지 여부를 big_bit로 알게되는데 그 계산의 원리는 다음과 같다.
총 11개의 bit가 있다. 011 1111 1111. 그 중 하위 10개의 bit가 모두 1이다. 이때 값을 구하려면
2^0 + 2^1 + 2^2 + ... + 2^9 이런식으로 구해도 되지만,
2 ^ 10 - 1 로 바로 구할 수 도 있다.
그래서 전달 받은 bit_bit가 1 << 10 - 1이면 하위 10bit가 모두 설정되어 0 부터 9가 모두 존재 한다라는 것이다.
끝으로 memset 에 관해 살펴보면,
memset은 두번째 인자로 전달 받은 값을 1바이트 기준으로 하여 dest에 초기화 시킨다고 한다.
즉, 2를 전달하면 0x00000002로 각 element가 초기화 되는 것이 아니라, 0x02020202로 초기화가 된다고 한다.
그래서 0 또는 -1에 대해서만 우리가 원하는 대로 초기화가 된다.
0 = 0x(00)(00)(00)(00)
-1 = 0x(ff)(ff)(ff)(ff) 이기 때문이다.
