8424

static int N;
static list<int> graph[1001];
static queue<int> q;

static int solution(void)
{
	int x, y, ret;
	
	scanf("%d", &N);
	for (int i = 0; i < N; i++)
	{
		scanf("%d %d", &x, &y);
		graph[y].push_back(x);
		graph[x].push_back(y);
	}

	ret = N;
	for (int y = 1; y <= N; y++)
	{
		if (graph[y].size() == 1)
			q.push(y);
	}

	while (!q.empty())
	{
		y = q.front();
		q.pop();
		ret -= 1;

		x = graph[y].front();
		graph[y].pop_front();

		graph[x].remove(y);

		if (graph[x].size() == 1)
			q.push(x);
	}

	for (y = 1; y <= N; y++)
		graph[y].clear();

	return ret;
}

일단 입력으로 주어지는 그래프 자체에는 사이클이 존재한다.

 

일반적으로 사이클이 존재하려면 적어도 하나의 정점은 최소 두개의 간선을 가져야 한다.

간선이 하나만 있으면 되돌아 올 수 없기 때문이다.

 

그래서 아래와 같이 생각해 볼 수 있다.

위 경우에서 모든 정점은 두개의 간선을 갖게 된다. 즉, 모든 곳에서 사이클이 발생할 수 있음을 뜻하고,

그 때의 사이클의 길이는 정점의 개수와 같다.

 

1번 정점은 간선의 개수가 하나이다. 즉 해당 정점을 제거하고 생각해야 사이클의 길이를 알 수 있다.

차수가 1인 정점은 하나 이므로 사이클의 길이는 4 - 1 = 3 이 된다.

 

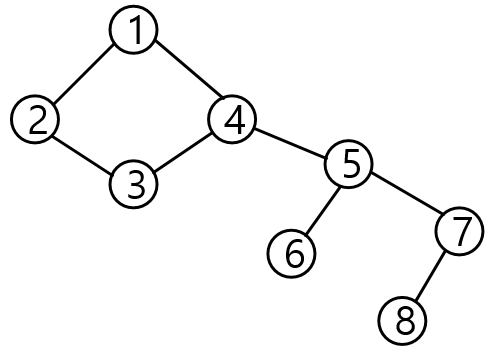
위 그래프에서 5번과 7번 정점은 차수가 2이상이지만 해당 정점에서는 사이클이 형성되지 않는다.

차수가 1인 6, 8 번 정점과 각각 연결되어 있기 때문이다.

그래서 6번과 8번을 제거하면 5번의 차수는 2, 7번의 차수는 1이된다. 차수가 1이 되었기 때문에 7번 정점을 제거하고 나면, 5번 정점의 차수는 다시 1이된다. 이 정점을 제거하고나면,

남은 정점들 중 차수가 1인 것은 없게 된다.

 

즉, 차수가 2이상인 정점의 개수가 곧 사이클의 길이가 된다.