static double p;
static long long N;
static double solution(void)
{
scanf("%lf %lld", &p, &N);
double ret = p, priv = p;
if (p == 1.0)
return (double)(N % 2);
else if (p == 0.0)
return 0.0;
else if (N >= 5462564)
return 0.5;
for (int i = 2; i <= N; i++)
{
ret = p + (1 - 2 * p) * priv;
if (ret == 0.5)
break;
priv = ret;
}
return ret;
}먼저 N번째 확률의 점화식을 구해보겠다.
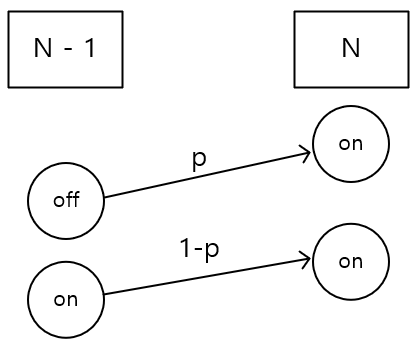
N번째에서 전구가 켜져있으려면, 위 그림처럼
N-1번째에서 off 되어 있다가 스위치가 p의 확률로 작동하는 경우와
N-1번째에서 on 되어 있다가 스위치가 1-p의 확률로 작동하지 않아야 한다.
그래서 N번째에서 전구가 켜져있을 확률을 f(n)이라 하고, 켜져 있지 않을 확률을 g(n)이라 한다면,
f(n) = f(n - 1) * (1 - p) + g(n - 1) * p, f(0) = 0, n >= 1 이다.
그리고 g(n) = 1 - f(n) 이므로,
f(n) = p + (1 - 2p) * f(n - 1) 이 된다.
그리고 입력으로 주어지는 p는 0 이상 1이하이다.
그래서 p = 0, p = 1 에 대해 계산을 해보면,
p = 0; -> f(n) = 0
p = 1; -> f(n) = 0, n is even, f(n) = 1, n is odd 임을 알 수 있다.
그리고 위 점화식에서 f(n)의 극한값을 a라 한다면, f(n-1)의 극한값도 a 이므로
a = 1/2 = 0.5 라는 것을 알 수 있다.
즉, n이 커지면 커질 수록 위 점화식은 0.5를 향해 다가가는 것이다.
그래서 그 n값을 찾아봤다.
입력으로 주어질 수 있는 성공확률 중 가장 높은 값은 0.999999이다.
그래서 이 값이 0.5에 가장 가까이 갈 때 까지 얼마나 걸리나 살펴보았다.
차이가 0.000009가 될 때는 5462564 였다.
(절대오차 혹은 상대오차가 10^-6 이하인 경우 정답으로 인정되기 때문이다.)
확률이 가장 낮은 0.000001도 같은 값이었다.
그래서 이 값 이상인 경우에 대해서는 무조건 극한값인 0.5를 반환하도록 하였고,
낮은 경우에는 직접 찾는 식으로 코드를 작성하였다.

