[1. 문제 설명]
- 그래프는 정점과 간선으로 이루어져 있다.
- 두 정점 사이에 경로가 있다면, 두 정점은 연결되어 있다고 한다.
- 연결 요소는 모든 정점이 서로 연결되어 있는 정점의 부분집합이다.
- 그래프는 하나 또는 그 이상의 연결 요소로 이루어져 있다.
- 트리는 사이클이 없는 연결 요소이다.
- 트리는 정점이 n개, 간선이 n-1개 있다.
=> 정점이 n 개 간선이 n-1 개 인 그래프는 트리이다? => FALSE - 트리에서 임의의 두 정점에 대해서 경로는 유일하다.
그래프가 주어졌을 때, 트리의 개수를 세는 프로그램을 작성하시오.
[2. 풀이 접근]
A. DFS
무방향 연결 그래프에서 임의의 트리를 하나 만들 수 있다.
어떤 정점에서 DFS 로 그래프를 한번 순회하면 된다. (혹은 BFS)
트리에서 임의의 두 정점의 경로는 유일하다는 특징을 이용 한 것이다.
DFS 나 BFS 모두 한번 방문했던 점은 다시 방문하지 않기 때문이다.
그런데 여기서 중요한 점은 그래프 내 Cycle 이 존재 할 수 있다는 것이다.
따라서, DFS 중 Cycle 의 존재를 알아내야 한다.
Cycle 은 아래와 같은 형상을 갖는다.

1번에서 출발한 경로가 같은 Edge 를 거치지 않고 다시 돌아오는 것과 같은 경우를 말한다.
입력으로 주어진 그래프는 무방향 그래프이므로,
(또 트리는 무방향 그래프이어야 한다, 부모->자식, 자식->부모로 갈수 있어야 하므로)
1 에서 2를 방문하면, 2는 다시 1로 갈 수 있다.
그러나 이 경우는 Cycle 로 간주하지 않고.
1->2->3 을 방문하고, 3에서 1로 가려는 순간 Cycle 을 찾았다고 할 수 있다.
이것을 정리하면
from -> to 로 방문하려 하는데, to 가 from의 부모 인 경우 cycle 임을 검출 할 수 있다.
그렇다면, dfs 중 cycle 을 검출하면
바로 종료하는 것이 맞을 까 아니면,
cycle 이 있음을 알고, 계속 dfs 를 진행하는 것이 맞을까 고민을 해봤는데,
이것은 그렇게 중요하지 않다.
아래와 같은 그래프를 고려해보면,
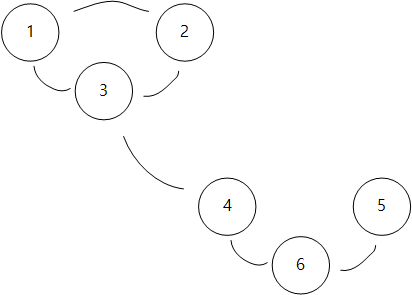
1에서 시작한 dfs 가 3에서 cycle 임을 알고 종료하고,
4에서 dfs 를 시작한 순간, 4는 인접한 3을 확인하는데,
4->3 을 방문하려는데, 3은 4가 아닌 부모 1인 것을 확인 할 수 있게 되므로
노드 4는 Cycle 인 그래프를 포함하게 되고,
결국 Tree 가 아니게 된다고 볼 수 있다.
B. Union Find
=> 나중에...
== 기타 출력에서 실수했던 사항 ==
문제를 잘 읽지 않은 것.
- Tree 의 개수가 2 이상인 경우 이 값을 출력해야 하는데, 3 이 고정되어 출력되고 있었던 것
- Case 1, 2, 3 은 Test Case 번호인데, 각각 tree 개수가 2 이상, 1개, 없는 경우에 대한 경우로 처리했던 점.
[3. 코드]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| Union-Find. [1976] (0) | 2022.10.04 |
|---|---|
| Union-Find. [1717] (0) | 2022.10.04 |
| 트리. [5639] (0) | 2022.10.02 |
| 트리. [2263] (0) | 2022.10.02 |
| 트리. [1991] (0) | 2022.10.02 |