[1. 문제 설명]
매 게임 시작 시 건물을 짓는 순서가 주어진다.
선행 건물을 모두 지어야 지을 수 있는 건물이 존재한다.
어떤 건물(W) 을 지을 때 까지 필요한 최소시간을 구한다.
[2. 풀이 접근]
건물을 짓는데 필요한 순서가 존재하므로, 위상 정렬로 접근 할 수 있다.
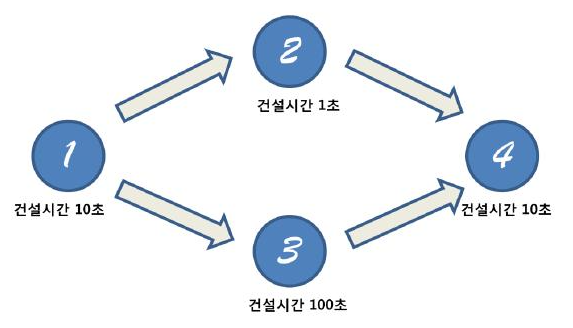
위의 예시에서 4번 건물을 짓는데 필요한 시간은
모든 선행 건물 들 중 가장 마지막에 지어지는 건물에 영향을 받는다.
또한 선행 건물들 역시 그 선행 건물들에 영향을 받으므로, (재귀적으로도 볼 수 있다.)
탐색 중 각 건물을 건설하기 위한 최대 시간을 갱신해야 한다.
위 그림에서는 3번이 2번보다 늦게 지어지지만, 아래 그림에서는 2번이 더 늦게 지어질 수 있기 때문이다.

== 풀이2, 동적계획법 ==
위상 정렬 접근 계획 중, 재귀적인 특성이 있다는 것을 확인하였다.
위상 정렬 은 선행 건물이 없는 건물부터 시작하지만,
재귀적인 특성을 고려하여 풀이를 한다면,
거꾸로 4번 건물부터 시작해야 한다.
(이 경우는, to 를 기준으로 from 을 알아야 하는데,
역방향 그래프를 만들거나
인접행렬로 해야 가능하다.)
4번에서 인접한 2번과 3번 역시 같은 재귀적인 방식으로 접근하여
둘 중 최대 시간이 걸리는 것을 찾고,
4번 건물을 짓는데 필요한 시간을 더하면 된다.
[3. 코드 - 위상정렬]
[3. 코드 - 동적계획법]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| 최소 공통 조상. [3584] (0) | 2022.10.22 |
|---|---|
| 위상 정렬. [16169] (0) | 2022.10.21 |
| 위상 정렬. [14567] (0) | 2022.10.20 |
| 위상 정렬. [3665] (0) | 2022.10.18 |
| 위상 정렬. [2252] (0) | 2022.10.17 |

