[1. 문제 설명]
https://algospot.com/judge/problem/read/CHILDRENDAY
[2. 풀이 접근]
먼저 모든 어린이들에게 같은 수의 장난감을 주고,
욕심쟁이 어린이들에게는 원래 가진 것에서 하나 씩 더 주면 1차적인 조건을 만족 시킬 수 있다.
그래서 구하고자 하는 c 는 아래와 같은 조건이 성립한다.
- n + m 이상이다.
- c = kn + m 형태로, c 를 n 으로 나눈 나머지는 m 이다.
- d 에 포함된 숫자로만 구성되야 한다.
위와 같이 여러 조건을 동시에 만족하면서 답을 찾아야 할 때
일부 조건을 없앤 더 단순한 문제를 푼 후, 조건을 하나씩 추가해 가는 전략이 있다.
- 단, 어느 조건을 무시하고 문제를 푸느냐에 따라 난이도가 달라 질 수 있다.
여기서는 1번 조건을 무시하고 진행해보기로 한다.
나머지 연산의 분배 법칙을 이용하면,
- 3번 조건을 만족하는 수로 만 답을 구성해가면서,
- 2번 조건을 만족하는 수를 찾을 수 있다.
구체적으로,
- d 에 포함된 숫자 중 하나를 이용하여, 최초 값을 만들고,
- 여기에 10 을 곱하고, d 에 포함된 숫자를 하나 더하는 과정을 반복해 가면서,
=> 최초 0 에서 출발,
=> d 에 포함된 숫자 중 a 를 이용하면, 0*10 + a == a 가 되고,
=> 위와 같은 과정을 반복하면, abcd,,, 등을 만들어 갈 수 있다. - 여기서, 아래 식을 만족하는지 확인 하는 것이다.
- (c X 10 + x) mod n == ((c mod n) X 10 + x)) mod n
- c 와 n 은 알 수 있는 값이므로, 미지수 x 를 구할 수 있다.
이제 그래프를 이용하여 모델링을 진행한다.
- 현재까지 구한 c 를 n 으로 나눈 나머지를 정점으로 표현한 방향 그래프를 만들 수 있다.
- 그래서 정점은 총 [0 ~ n-1] 인 n 개의 정점이 존재하게 된다.
- 어떤 정점 a 가 있고, 이는 현재까지 구한 c 를 n 으로 나눈 나머지가 a 라는 의미가 된다.
- 여기서, c 의 뒤에 숫자 x 를 붙이면, 나머지는 (10a + x) mod n 으로 바뀌게 된다.
=> 이 나머지를 b 라고 하면, - 그래서 a -> b 는 서로 연결되고, a 에서 b 로 가는 edge 에 x 라는 값을 부여 할 수 있다.
이렇게 그래프를 만들고 나면, 0 에서 m 으로 가는 최단 경로에 의미는 아래와 같다.
- 조건2 와 3 을 만족하는 가장 짧은 길이의 c
- 여기서 c 는 숫자로만 구성된 문자열.
하지만 이러한 경로가 여러 개인 경우가 있을 수 있다.
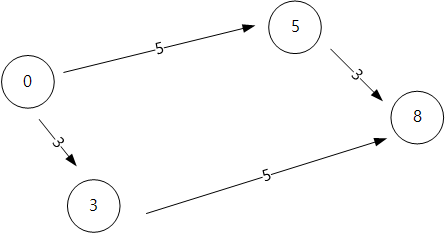
가령, 0 - 3 - 8 과 0 - 5 - 8 중, 최소 값을 구하려면 0 - 3 - 8 을 선택해야 한다.
- 간선 번호를 보면
=> 0-3-8 은 3,5
=> 0-5-8 은 5,3
이므로, 35가 최소 값이다.
즉, edge 를 사전순으로 가장 작은 최단 경로를 찾아야 한다.
이 부분은 현재 상태에서 다음 상태로 가야 할 때,
d 에 포함된 숫자를 사전순으로 사용하도록 하면 된다.
위와 같은 상황에서, bfs 특성 상, 0 ~ 8 로 가야 할 때,
문자열 d 가 35 라면,
- 0 에서는 3 , 5 순서대로 사용하고나면,
- 8 에 먼저 도달하는 것은, '정점 3' 에서 '간선 5' 를 이용하여 먼저 방문하기 때문에
- '정점 5' 에서 '간선 3' 을 이용하여 방문 할 수 없게 되기 때문이다.
이제, 2번과 3번 조건을 만족하면서 최소 값은 c 를 구할 수 있고,
마지막으로 1번 조건을 만족해야 한다.
만약 문제에서 m = 0 으로 주어진다면,
0 에서 0 으로 가는 최단 경로를 찾게 되고,
이 때 답은 0 이 되어, 모든 어린이들에게 최소 하나의 장난감을 주지 못하게 된다.
이러한 상황을 막기위해서는 그래프를 한바퀴 돌아오는 경로를 찾아야 한다.
그리고 이 때에는, 시작점인 0과 한바퀴 돌아서 도착한 0은 같은 정점일 수 없다.
- 시작점 0 은 현재 가진 값이 n 미만이고
- 한바퀴 돌아서 도착한 0 은 현재 가진 값이 n 이상이기 때문이다.
그래서 나머지를 구할 때,
현재까지 계산 한 c 가 n 이상인 경우를 고려하여 계산하도록 한다.
그림도 좀 필요할 것 같은데,,,,
나머지는 코드 주석을 참조하도록 한다.
[3. 코드]
