[1. 문제 설명]
2-SAT 는 N 개의 boolean 변수가 있을 때,
2-CNF 식을 true 로 만들기 위해 xi 를 어떤 값으로 정해야하는지를 구하는 문제이다.
2-CNF 식은 아래와 같은 형태이다.
f = (x ∨ y) ∧ (¬y ∨ z) ∧ (x ∨ ¬z) ∧ (z ∨ y)
N 개의 변수가 있고, M 개의 절이 주어질 때,
식 f 를 true 로 만들 수 있다면 1,
없다면 0을 출력한다.
[2. 풀이 접근]
각 절(clause) 들이 모두 true 가 되어야, 전체 식 f 가 true 가 된다.
p ∨ q 를 참으로 하는 명제는 아래와 같다.
- !p -> q
- !q -> p
정리하면, p 와 q 둘 중 적어도 하나는 true 이어야 한다.
p 가 true 이면, q 는 어느 값이어도 상관이 없다.
역시 q 가 true 이면, p 는 어느 값이어도 상관이 없다.
이제, 입력으로 주어지는 각 절을 위와 같이 방향그래프로 표현하도록 한다.
그러면, 각 절마다 두개의 edge 가 생성된다.
이런 방식으로 전체 절을 이용하여 그래프를 구성한다.
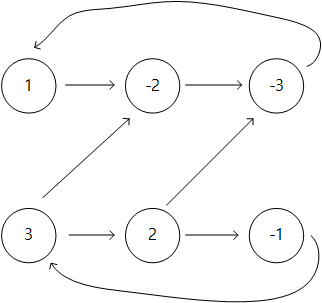
각 절이 true 가 되도록 edge 를 구성하였으므로,
같은 SCC 에 속한 노드들은 논리적 모순이 없어야 한다.
p -> q 이고 q -> r 이 성립하면, p -> r 도 성립해야 하는 것 이다.
그러나 특정 상황에서 전체 식이 true 가 될 수 없게 되는데,
그 상황은 xi ~> ¬xi 와 ¬xi ~> xi 인 path 가 모두 존재하는 경우이다.
xi 를 가정하였는데, ¬xi 가 추론된다던가
¬xi 를 가정하였는데, xi 가 추론되는 경우는 모순인 상황이기 때문이다.
즉, xi 와 ¬xi 가 같은 scc 에 속한 경우가
(같은 SCC 에서는 Cycle 이 형성된다.)
모순된 상황을 의미하며, 식 f 를 true 로 만들 수 없는 경우를 나타낸다.
[3. 코드]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| SCC. [3648] (0) | 2022.11.29 |
|---|---|
| SCC. [11281] (0) | 2022.11.28 |
| SCC. [4013] (0) | 2022.11.27 |
| SCC. [3977] (0) | 2022.11.27 |
| SCC. [4196] (0) | 2022.11.27 |

