[1. 문제 설명]
함수가 아래 두 조건을 만족 할 때,
f1(x) = f(x)
fn+1(x) = f(fn(x))
fn(x) 를 계산한다.
[2. 풀이 접근]
처음에 생각했던 방식은 x 에서 f(x) 로 가는 그래프를 만들고,
dfs 로 풀이하는 방법이었다.
(단, cycle 이 발생하거나, 연결된 노드가 자기자신인 경우에 대해서 예외 처리를 추가해서)

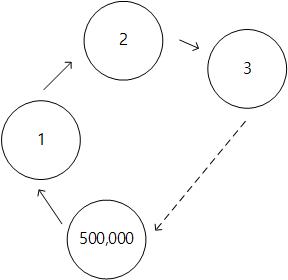
그러나 아래와 같이 그래프가 원을 이루는 경우는 입력의 최대에 대해서
매번 500,000 번의 탐색을 진행해야 하기에 시간초과가 발생할 것이라 생각하였다.
Sparse table
sparse table 이란 자료구조는 아래 두가지 조건이 성립한 경우 사용 할 수 있다.
- 대응되는 값(함수 값) 이 변하지 않는다.
- 함수는 결합 법칙이 성립해야 한다.
=> f(a, b, c) = f(a, f(b, c)) = f(f(a, b), c)
https://namnamseo.tistory.com/entry/Sparse-Table
탐색 시간 복잡도 => O(nlogn)
문제에서 제시 된 함수는 이 두가지 조건을 만족한다.
n 을 1과 거듭제곱 형태로 분리하여, sparse table 을 사용 할 수 있다.
(bit 단위로 바라보면 된다.)
[3. 코드]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| 최소 공통 조상. [3176] (0) | 2022.10.25 |
|---|---|
| 최소 공통 조상. [11438] (0) | 2022.10.24 |
| 최소 공통 조상. [3584] (0) | 2022.10.22 |
| 위상 정렬. [16169] (0) | 2022.10.21 |
| 위상 정렬. [1005] (0) | 2022.10.21 |



