[1. 문제 설명]
최대 100,000 개의 노드로 이루어진 트리가 주어진다.
루트는 1번 노드이다.
두 노드의 쌍이 최대 100,000 개 가 주어질 때,
두 노드의 가장 가까운 공통 조상을 출력한다.
[2. 풀이 접근]
이전에 풀었던 방식(https://testkernelv2.tistory.com/395?category=536991)으로 진행 할 경우
이번 문제에서는 O(N2) 이 걸린다.
N 의 최대가 100,000 이므로 시간 초과가 발생 할 것이다.
root 는 이미 주어져 있고,
dfs 를 통해 각 노드의 부모 및 높이를 설정하는 부분 까지는 동일하다.
(이번 문제에서 주어지는 edge 는 부모-자식을 의미하지 않는다.)
여기서 시간이 오래 걸리는 부분은
- 노드의 높이를 맞추는 부분
- 공통 조상까지 거슬러 올라가는 부분
이 두 부분을 최적화 해야한다.
노드가 부모로 거슬러 올라가는 부분에 sparse table 을 적용 할 수 있다.
1번 과정에서 높이를 맞추는 부분을 1씩 올라가지 말고,
sparse table 을 이용하여 최대 20 단계에 걸쳐 올라 갈 수 있다.
(220 = 대략 1,000,000 > 100,000)
2번 과정에서 공통 조상을 찾는 부분에 대해서는 이진 탐색을 고려해볼 수 있다.
low=0, high=100,000 범위 내에서 올라갈 횟수를 이분법으로 선택해서
최종적으로 u 와 v 가 같아지는 경우 high 를 mid-1 로 낮춰서,
u 와 v 가 일치하지 않는 경우 low 를 mid+1 를 높여서 진행 해보는 것이다.
== 더 최적화 하기 ==
위에서 정리한 방법으로는 문제를 해결 할 수는 있지만,
제한 시간에 거의 딱 맞춰서 풀린다.
(이분 탐색하는 곳에서 오래 걸리는 듯?)
약간 다르게 생각해서 높이가 같은 두 노드에서 가장 먼 공통 조상은 언제나 root 일 것이다.
220 == 1,000,000 이니 sparse table 에서 220 번 올라간 두 노드의 조상은 root 1 이다.
여기서 210 번 올라간 두 노드의 조상이 다를 경우,
LCA 는 210 과 220 사이에 존재한다고 볼 수 있다.
=> 당연하게도 210 이전에 LCA 가 존재할 수 는 없으며,
=> 두 노드가 LCA 가 된 노드에서 더 위로 올라가면 항상 같은 노드가 되게 된다.
즉, 두 노드의 2k-1 이후 부모 노드가 달라지는 시점에서 u 와 v 를 업데이트 해야한다.

u 와 v 의 LCA 가 p 라고 한다면,
p 이후로는 항상 같은 공통 조상을 같게 된다.
여기서 p 는 2k 번 위로 올라간 곳에 위치 할 수 있거나
2k 와 2k-1 사이에 위치한 곳에 존재 할 수 있다.
하지만, 적어도 u 와 v 에서 2^k 번 보다 위로 올라간 곳에서는 항상 같은 조상 노드를 갖게 된다.
그래서 u 와 v 를 2k-1 번 위로 올려주고,
여기서 다시 탐색을 하게 하면 된다.
단, 여기서 탐색 범위를 다시 늘릴 필요는 없다.
(=> k 를 다시 20 부터 할 필요는 없다)
2k 와 2k-1 사이의 범위 (= 2k) 는
[2k-2, 1] 사이의 모든 범위(2의 거듭제곱에 한하여) 를 더한 것과 같기 때문이다.
=> 2K-2 + 2K-3 + ... + 1
=> 항의 개수는 K-1 이다. (등비수열 합)
위 과정을 마치고 나면 u 와 v 그리고 LCA 는 아래와 같은 구조를 갖게 된다.
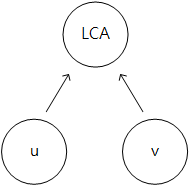
각 노드에서 한번만 더 올라가면 LCA 를 찾게 된다.
u 와 v 를 업데이트 하는 순간은 u 와 v 의 부모가 서로 다를 때 였기 때문이다.
[3. 코드 - 1]
[3. 코드 - 2]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| 최소 공통 조상. [13511] (0) | 2022.10.26 |
|---|---|
| 최소 공통 조상. [3176] (0) | 2022.10.25 |
| Sparse table. [17435] (0) | 2022.10.23 |
| 최소 공통 조상. [3584] (0) | 2022.10.22 |
| 위상 정렬. [16169] (0) | 2022.10.21 |



