[1. 문제 설명]
N 개의 정점과 N-1 개의 edge 로 이루어진 네트워크가 존재
모든 정점 쌍에는 두 정점을 연결하는 유일한 경로가 존재
edge 의 거리가 주어짐
K 개의 정점 쌍이 주어질 때,
두 정점을 연결하는 경로 에서 가장 짧은 edge 의 길이와 가장 긴 edge 의 길이를 출력한다.
[2. 풀이 접근]
먼저 주어지는 그래프는 Tree 라는 것을 알 수 있다.
- N 개의 정점과 N-1 개의 edge 가 존재
- 임의의 두 정점을 연결하는 경로가 유일함
여기서 두 정점을 연결하는 경로는 두 정점의 최소 공통 조상까지 연결되어 있다.
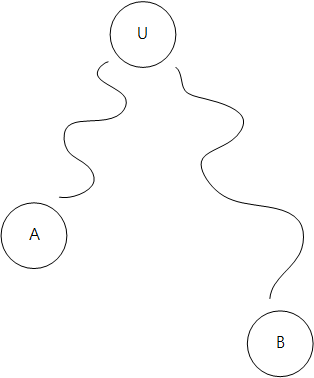
B 에서 A 를 잇는 경로는 B 에서 출발하여 위로 계속 올라가다가
최소 공통 조상(LCA) U 에서 다시 아래로 내려가는 경로라는 것을 알 수 있다.
즉, B 에서 LCA 사이 edge 와
A 에서 LCA 사이 edge 중 거리가 최대, 최소인 것을 찾으면 된다.
먼저 B 에서 LCA 사이 edge 중 최소를 찾는 문제는 아래와 같이 접근할 수 있다.

v1 에서 4번 이동한 경로에서 최소 edge 는
=> v1 에서 2번 이동한 경로에서 최소 edge 와
=> v3 에서 2번 이동한 경로에서 최소 edge 중 최소 값 이다.
==> minDists[2][v1] = min( minDists[1][v1] , minDists[1][v3] )
= min( minDists[1][v1], minDists[1][parents[1][v1]] )
LCA 를 찾기 위한 sparse table 개념을 최소 edge 를 찾기 위한 곳에도 적용 할 수 있다.
이러한 방식으로 최대 edge 역시 구할 수 있다.
마지막은 LCA 를 찾기 위해 먼저 root 를 찾는 방법이다.
문제에서 주어지는 입력은 tree 구조를 하고 있지만,
두 노드 중 어느 것이 부모인지 알려주지 않으며,
또한 별도 root 를 정하지 않는다.
(그래서 양방향으로 그래프를 생성하도록 한다.)
이 경우 그냥 아무 단말노드를 root 로 잡으면 된다.
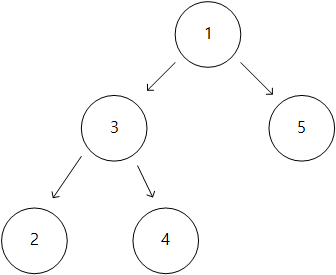
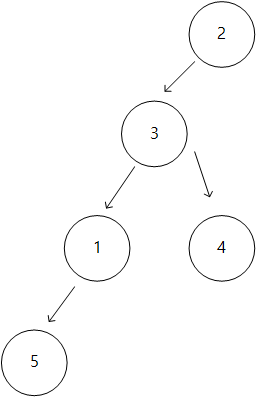
아래 그림에서 1번을 root 로 할 경우 균형잡힌 트리로 볼 수 있다.
그러나 2번을 root 로 할 경우 역시 균형잡히지는 않았지만, 역시 tree 로 볼 수 있기 때문이다.
leat node 는 edge 가 한개 이므로 쉽게 찾을 수 있다.
[3. 코드]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| 구간 트리. [2042] (0) | 2022.10.27 |
|---|---|
| 최소 공통 조상. [13511] (0) | 2022.10.26 |
| 최소 공통 조상. [11438] (0) | 2022.10.24 |
| Sparse table. [17435] (0) | 2022.10.23 |
| 최소 공통 조상. [3584] (0) | 2022.10.22 |


