[1. 문제 설명]
N 개의 정점으로 이루어진 트리가 주어졌을 때,
임의의 경로에 대해서
A. 경로의 비용을 출력
B. u->v 로 가는 경로에서 k 번째 정점을 출력 하도록 한다.
[2. 풀이 접근]
경로의 비용을 sparse table 의 형태로 저장 할 수 있으며,
u->v 의 LCA 를 찾는 과정에서 u->v 경로의 비용을 찾을 수 있다.
참조=> https://testkernelv2.tistory.com/398
경로의 k 번째 정점을 찾는 부분이 살짝 까다로웠다.
일단 LCA 를 찾는 것이 먼저이다.
u -> LCA
v -> LCA 간 높이 차이를 이용하여 k 가 어디에 있을 지 추정 할 수 있기 때문이다.
처음에 생각한 방법은 오답이었다.
- u 와 LCA 간 높이차이를 계산 = height1
- v 와 LCA 간 높이차이를 계산 = height2
- 경로를 구성하는 노드의 개수를 계산 = height1 + height2 + 1
- u - k 까지 거리와 k - v 까지 거리 중 최소를 선택
- 선택 된 노드에서 k 까지 거슬러 올라감

u ~ lca - v 에 이르는 경로를 일렬로 늘리면, 우측의 그림과 같이 되고,
u 는 순서 상 1,
v 는 순서 상 노드 개수 가 된다.
기본적으로 거슬러 올라갈 노드를 u 라하고,
v-k 차이가 u-k 차이보다 더 작을 때 거슬로 올라갈 노드를 v 로 바꿀 때
아래와 같은 반례가 있어서 오답이 된다.

1 -> 7 로 가고, 4번째 노드일 때
1 -> 4 차이는 3
4 -> 7 차이는 3
둘이 같으므로, 1번 노드에서 3번 올라가게 되며,
이는 답인 4 가 아니라 root 가 된다.
== 올바른 풀이 ==
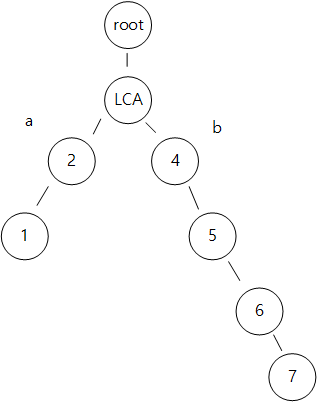
같은 예제로 다시 돌아와서 k 가 위치할 수 있는 곳은
a 또는 b 에 있을 수 있다.
k 가 a 에 있으려면 u->LCA 높이 차 이내에 존재해야 하고,
k 가 b 에 있으려면 u->LCA 높이 차 보다 커야 한다.
추가로 k가 a 에 있기 위해서 주의해야 할 점은
k 가 LCA 까지 되도 된다는 것이다.

위 그림에서 1 -> 4 경로에서, 3번째 노드를 찾을 때 (k=3),
u 와 LCA 간 높이차이는 3 이다.
그러나 경로 상에는 총 4개의 노드가 존재 할 수 있다.
따라서 조건을 if ( k <= height1 + 1 ) 일 때 u 에서 LCA 로 높이차이 만큼 올라가야 한다.
이번에는 k 가 v 경로 상에 오는 경우이다.

1-> 6 경로에서 , 5번째 노드를 찾을 때 (k=5)
6 에서 k 까지 높이 차를 구해야 한다.
이 높이 차는 6->LCA 까지 높이 차(=h2) 에서 K->LCA 까지 높이 차(=h1) 를 빼면 된다.
여기서 h1 은 1->K 까지 경로의 길이에서 1->LCA 까지 높이 차(=h0) 를 빼서 구할 수 있다.
[3. 코드]
'알고리즘 > Baekjoon' 카테고리의 다른 글
| 구간 트리. [11505] (1) | 2022.10.29 |
|---|---|
| 구간 트리. [2042] (0) | 2022.10.27 |
| 최소 공통 조상. [3176] (0) | 2022.10.25 |
| 최소 공통 조상. [11438] (0) | 2022.10.24 |
| Sparse table. [17435] (0) | 2022.10.23 |

